Deep-learning algorithms are helping us overcome a wide variety of computer vision problems. While extremely useful they have a number of drawbacks, one being that they are trained on data to be used in a specific domain or use case. Apply the model to another problem for which it was not designed, and it usually fails miserably. Retraining the model for another use case takes a lot of time and, in many cases, may not be feasible.
Learning paradigms designed for multiple domains or tasks, such as multitask learning, continual learning and domain adaptation, aim to reduce the large amount of energy and manual labor needed to retrain machine learning models. In this work, we introduce a domain adaptation approach that exploits learned features from relevant source tasks to reduce the data required for learning the new target task.
The need for learning from multiple tasks
A task refers to a conventional supervised learning problem: given labeled data taken from the input and output spaces, we either maximize a performance measure or minimize a loss function. Multitask learning focuses on the joint learning of tasks. Continual learning targets the sequential learning of tasks without forgetting what has been previously learned. Domain adaptation adapts machine learning models to different target domains while simultaneously training these models from related source domains.
Domain adaptation seeks to overcome scarcity of data in a target domain by utilizing the abundance of data available in related source domains. By achieving this, machine learning can adapt to different domains (domain adaptation). To explain further: In a source domain, the objective of the machine learning task is, for example, to recognize objects for which there is an abundance of training data. In the target domain, the objective of the task is to recognize those objects under different conditions for which there is no or very little training data.
While advances in deep learning paradigms are progressing, the training of new models is still extremely inefficient. It entails extra computational time and energy use.
We recently improved domain adaptation by incorporating our measure, von Neumann Conditional Divergence, into the learning objective along with our new method, Matrix-based Discrepancy Distance (MDD). Matrix-based Discrepancy Distance helps models learn from less data in the target domain by aligning and using features learned in related source domains.
Feature similarity for domain adaptation
Similar feature representations play a pivotal role in the success of solving problems for domain adaptation. Feature similarity includes both the invariance of feature marginal distributions and the closeness of conditional distributions given the desired response y (e.g., class labels). Unfortunately, traditional domain adaptation methods learn these features without fully taking into consideration the information in y . This can lead to a mismatch of the conditional distributions or a mix-up of discriminative structures underlying the data distributions. In this work, we incorporate our recently proposed von Neumann Conditional Divergence to improve the transferability of tasks across multiple domains.
The new divergence is differentiable and able to easily quantify the functional dependence between the learned features and y . Given multiple source tasks, we integrate this divergence to capture discriminative information in y . Assuming those source tasks are observed either simultaneously or sequentially, we can also design novel learning objectives.
Work by Yu et al.1 defines the relative divergence from P1(y|x) to P2(y|x) as:
DP1yxP2(y|x))= DvN(σxyρxy- DvN(σx|ρx) ,
where σxy and ρxy denote the sample covariance matrices of the joint distributions P1(y|x) to P2(y|x) , respectively. Similarly, σx and ρx refer to the sample covariance matrices of the marginal distributions P1(x) to P2(x) , respectively. DvN is the von Neumann divergence2, DvN (σρ) =Tr (σlogσ- σ log ρ - σ + ρ), which operates on two symmetric positive definite matrices, σ and ρ.
To align the conditional distributions of the output y given the features in the domain adaptation setting, we derive a symmetric von Neumann Conditional Divergence for the two matrices σxy and ρxy. We call this the Jeffery von Neumann Divergence and denote it as JvN(σxy:ρxy) . With this established, we show that the equation’s square root:
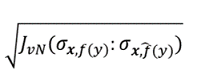
can be interpreted and used as a loss function that satisfies the triangle inequality, where:
f is the true labeling function, and the esimated predictor is:
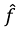
Satisfying the triangle inequality is necessary in order to derive a generalization bound for the target domain.
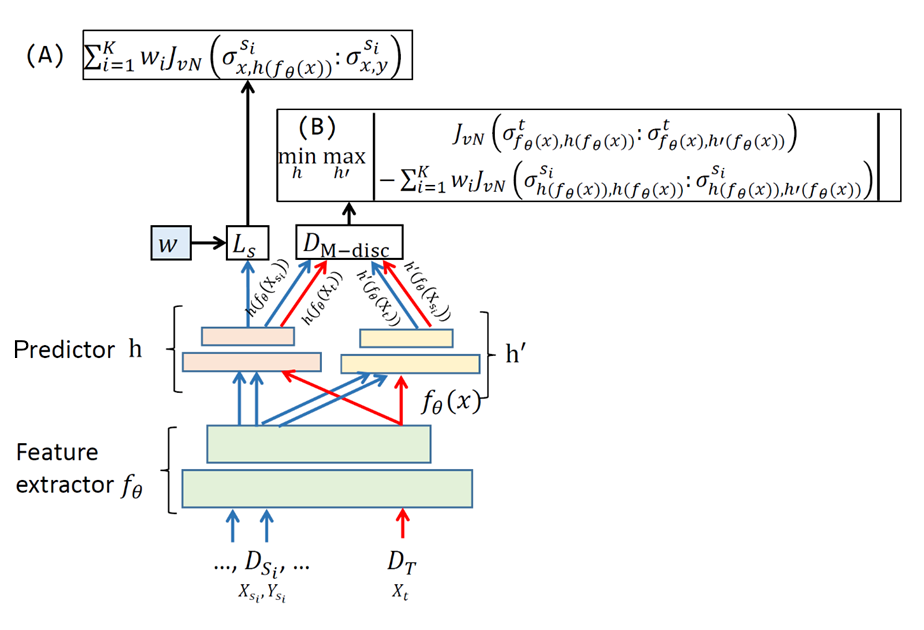
Figure 1 illustrates how the Jeffery von Neumann Divergence is employed in our new multisource domain adaptation method, Matrix-based Discrepancy Distance. In the figure, the objective includes two terms: A) minimization of the weighted risk from all source domains, i.e., Ls ; and B) minimization of the matrix-based discrepancy distance DM-disc between target distribution and the weighted source distribution. Dsi is the ith source domain, DT is the target domain, fθ is a feature extractor, h and h' are the predictor and the adversarial hypothesis, and wi is the weight of the source Di.
In our work, we define a matrix-based discrepancy distance DM-disc to quantify the discrepancy between two distributions P and Q over X based on our new loss, the square root of JvN . This distance reaches the maximum value if a predictor h' is very close to h on the source domain but far away from the target domain (or vice versa). Moreover, we bound the square root of JvN on the target domain Dt by quantities controlled by (i) a convex combination over the square root of JvN in each of the sources; (ii) the mismatch between the weighted distribution of the source domains and the target distribution; and (iii) the optimal joint empirical risk on the source and target domains.
We explicitly implement the idea exhibited by the bounding of the loss on the target domain and combine a feature extractor and a class predictor in a unified learning framework, as shown in Figure 1.
Vehicle counting as a domain adaptation problem
NEC’s technologies in computer vision and smart transportation are landmarks in the AI world. With our domain adaptation work, we have uncovered an opportunity to combine computer vision and aspects of smart transportation in a concrete application to count vehicles in traffic jams. Estimating vehicle count delivers vital information to enable the success of intelligent traffic management systems.
By using von Neumann Conditional Divergence and the Matrix-based Discrepancy Distance, we can now design machine learning models that predict the number of vehicles in different locations even when the types of cameras, lighting conditions and regions of interest are different. With our technology, cameras can be clustered into domains, and these domains used for multisource domain adaptation. See Figure 2, which clusters images taken from the TRaffic ANd COngestionS (TRANCOS)3 dataset, a public benchmark dataset for extremely overlapping vehicle counting. The dataset contains images that were collected from 11 video surveillance cameras that monitor different highways in the Madrid area, Spain. The empirical evaluations show that our method outperforms state-of-the-art methods in estimating the count of vehicles. For more details, read our recent paper on domain adaptation, Learning to Transfer with von Neumann Conditional Divergence (Shaker et al.)4.
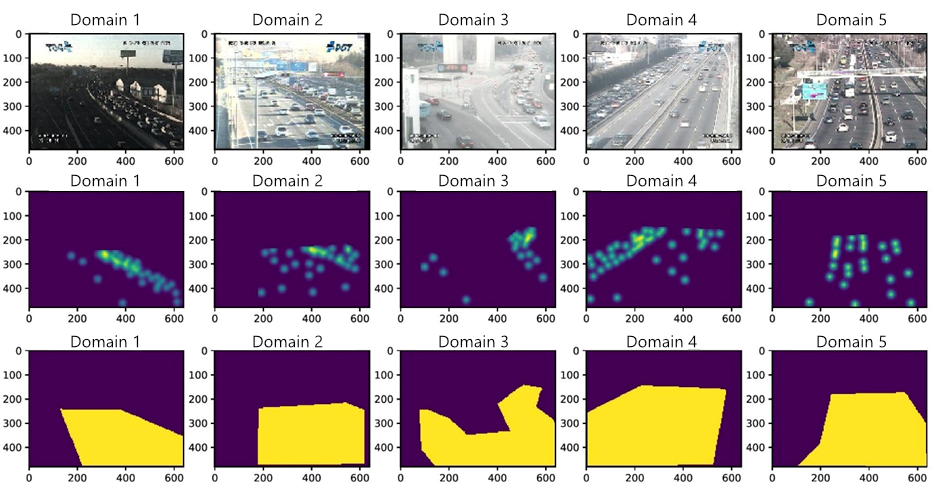
Figure 2 shows sample images, with their corresponding density maps and masks taken from the obtained domains. The ground truth images depicting the location of vehicles are turned into density maps by placing Gaussian kernels centered at each annotated location. The mask images show the road’s region of interest.
Conclusion
As this research shows, applying von Neumann Conditional Divergence and Matrix-based Discrepancy Distance increases the learning efficiency of deep learning models when applied to a concrete application. Empirical evaluations demonstrate that our method outperforms state-of-the-art methods in estimating the count of vehicles, even in traffic jams. This increased efficiency can, in turn, contribute to a significant reduction of computation requirements needed for the development of new deep-learning models.
This research was presented at last year’s 36th AAAI Conference on Artificial Intelligence in the paper “Learning to Transfer with von Neumann Conditional Divergence” by Ammar Shaker, Shujian Yu, and Daniel Oñoro-Rubio.
You can read more about this work in the preprint version of the research paper available on our website.
The Human-Centric AI Group
[1] Yu, S., Shaker, A., Alesiani, F., & Principe, J. C., “Measuring the discrepancy between conditional distributions: Methods, properties and applications,” IJACI, 2020.
[2] Nielsen, M. A., Chuang, I., “Quantum computation and quantum information,” American Association of Physics Teachers, 2002.
[3] Guerrero-Gómez-Olmedo, Ricardo, et al., "Extremely overlapping vehicle counting," Iberian Conference on Pattern Recognition and Image Analysis, Springer, Cham, 2015.
[4] Shaker, Ammar, Shujian Yu, and Daniel Oñoro-Rubio, "Learning to Transfer with von Neumann Conditional Divergence," Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 36 No. 8, 2022.